Programming Model

Nu+ Programming Model

Nu+ programming model

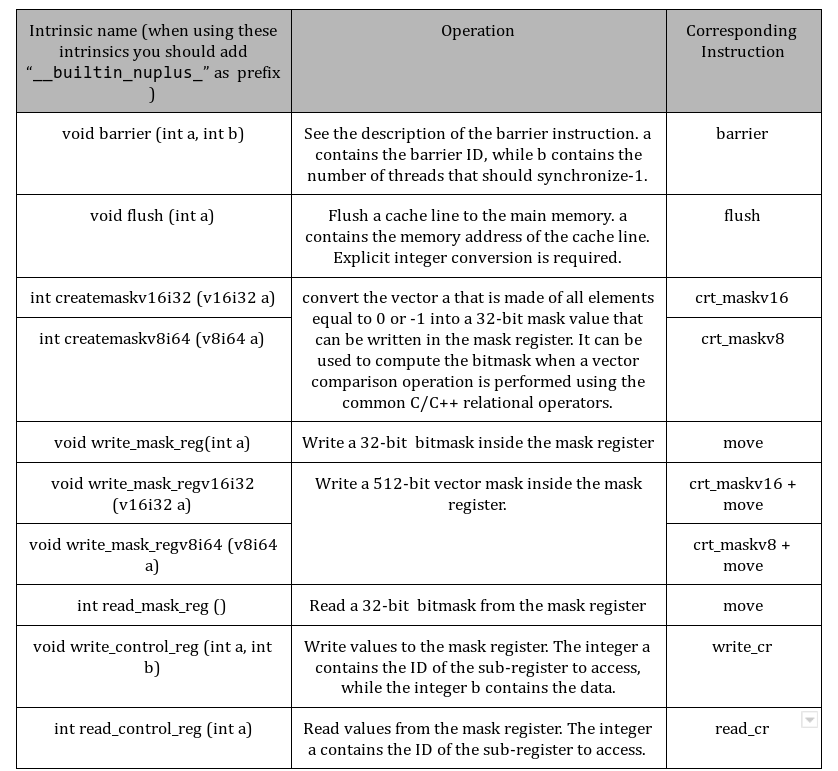
Nu+ Intrinsics

Matrix Multiplication Multithreaded Example

The following code shows a multithread version of the matrix multiplication kernel running on a nu+ core. The code spreads the output computation among all available threads. Since each output element computation is independent of others, the thread parallelism is achieved dividing the outer cycle of the function. Output matrix row calculations are equally spanned across all cores and further spanned across threads. For each thread, the function first calculates the portion of the output matrix to compute at the core level: N / CORE_NUMB, with N the dimension of the matrix and CORE_NUMB the number of nu+ core in the system. Then, each thread starts computing the outer loop with start_loop = (core_id * N / CORE_NUMB) + thread_id the portion of output matrix to compute is multiplied to the running core ID (core_id) and added to the running thread ID (thread_id), and each iteration increments by the number of threads in the core THREAD_NUMB.

void matrix_mult(const int a[N][N], const int b[N][N], int mult[N][N], int core_id, int thread_id) {
 int start_loop = (core_id * N / CORE_NUMB) + thread_id;
 int end_loop = N / CORE_NUMB * (core_id + 1);
 
 for (int i = start_loop; i < end_loop; i += THREAD_NUMB){
   for (int j = 0; j < N; j++)
     for (int k = 0; k < N; k++)
       mult[i][j] += a[i][k] * b[k][j];
 }
}

Parameters core_id and thread_id are passed by the main function, and fetched from nu+ control registerr through builtins:

#define CORE_ID    __builtin_nuplus_read_control_reg(0)
#define THREAD_ID  __builtin_nuplus_read_control_reg(2)

In this way, each thread in each core computes a portion of the output matrix concurrently to the others.

The final result is ready when all thread over the system ended the assigned task, a system synchronization is required and in the main function this is achieved using barrier builtin provided by the programming model:

__builtin_nuplus_barrier(42, CORE_NUMB * THREAD_NUMB - 1);

The builtin above synchronizes CORE_NUMB * THREAD_NUMB number of threads (total number of thread running in the system) on the ID 42. When all threads hit the barrier the output matrix is ready, although most of it could be in private L1 caches. The next step is to flush output lines into the main memory:

if (THREAD_ID == 0 && CORE_ID == 0) {
     for (int i = 0; i < N*N; i += 64 / sizeof(int)) {
       __builtin_nuplus_flush((int) &C[i / N][i % N]);
     }
     __builtin_nuplus_write_control_reg(N*N, 12); // For cosimulation purpose
   }

Generally, flush operations are performed by a thread, in this case the first thread in the first core calls the flush builtin which sends output results still in L1 caches to the main memory.

The full code for the main function is attached below:

#define CORE_ID    __builtin_nuplus_read_control_reg(0)
#define THREAD_ID  __builtin_nuplus_read_control_reg(2)

int main(){
   init_matrix(A);
   init_matrix(B);

   matrix_mult(A, B, C, CORE_ID, THREAD_ID);
   __builtin_nuplus_barrier(CORE_ID + 1, THREAD_NUMB - 1);

   if (THREAD_ID == 0 && CORE_ID == 0) {
     for (int i = 0; i < N*N; i += 64 / sizeof(int)) {
       __builtin_nuplus_flush((int) &C[i / N][i % N]);
     }
     __builtin_nuplus_write_control_reg(N*N, 12); // For cosimulation purpose
   }

  return (int)&C;
}

OpenCL support for Nu+

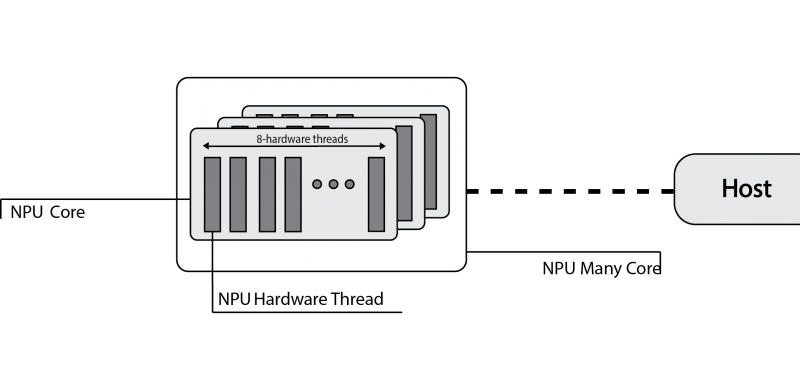
OpenCL defines a platform as a set of computing devices on which the host is connected to. Each device is further divided into several compute units (CUs), each of them defined as a collection of processing elements (PEs). Recall that the target platform is architecturally designed around a single core, structured in terms of a set of at most eight hardware threads. Each hardware threads competes with each other to have access to sixteen hardware lanes, to execute both scalar and vector operations on 32-bit wide integer or floating-point operands.

The computing device abstraction is physically mapped on the nu+ many-core architecture. The nu+ many-core can be configured in terms of the number of cores. Each nu+ core maps on the OpenCL Compute Unit. Internally, the nu+ core is composed of hardware threads, each of them represents the abstraction of the OpenCL processing element.

Execution Model Matching

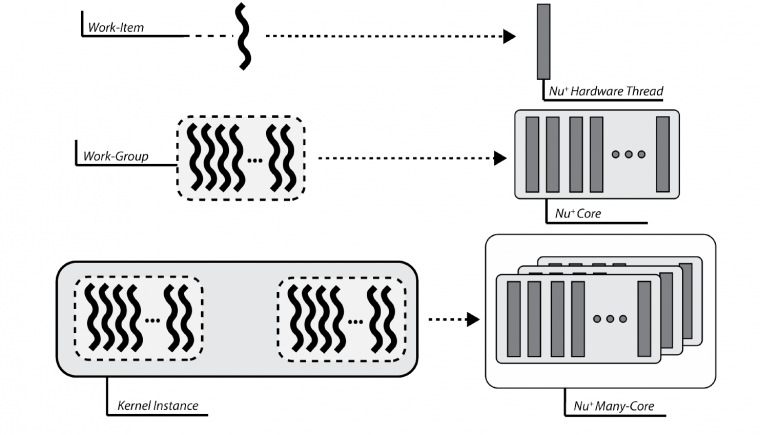
From the execution model point of view, OpenCL relies on an N-dimensional index space, where each point represents a kernel instance execution. Since the physical kernel instance execution is done by the hardware threads, the OpenCL work-item is mapped onto a nu+ single hardware-thread. Consequently, a work-group is defined as a set of hardware threads, and all work-items in a work-group executes on a single computing unit.

Memory Model Matching

OpenCL partitions the memory in four different spaces:

• the global and constant spaces: elements in those spaces are accessible by all work-items in all work-group.
• the local space: visible only to work-items within a work-group.
• the private space: visible to only a single work-item.

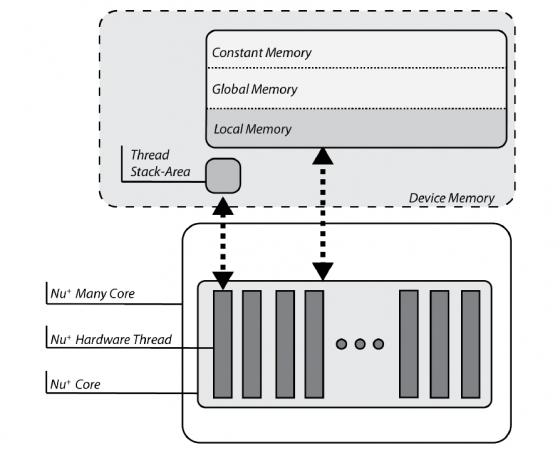
The target-platform is provided of a DDR memory, that is the device memory in OpenCL nomenclature. Consequently, variables are physically mapped on this memory. The compiler itself, by looking at the address-space qualifier, verifies the OpenCL constraints are satisfied.

Each nu+ core is also equipped with a Scratchpad Memory, an on-chip non-coherent memory portion exclusive to each core. This memory is compliant with the OpenCL local memory features

Finally, each hardware thread within the nu+ core has a private stack. This memory section is private to each hardware thread, that is the OpenCL work-item, and cannot be addressed by others. As a result, each stack acts as the OpenCL private memory.

Programming Model Matching

OpenCL supports two kinds of programming models, data- and task-parallel. A data-parallel model requires that each point of the OpenCL index space executes a kernel instance. Since each point represents a work-item and these are mapped on hardware threads, the data-parallel requirements are correctly satisfied. Please note that the implemented model is a relaxed version, without requiring a strictly one-to-one mapping on data.

A task-parallel programming model requires kernel instances are independently executed in any point of the index space. In this case, each work-item is not constrained to execute the same kernel instance of others. The compiler frontend defines a set of builtins that may be used for this purpose. Moreover, each nu + core is built of 16 hardware lanes, useful to realise a lock-step execution. Consequently, OpenCL support is realised to allow the usage of vector types. As a result, the vector execution is supported for the following data types:

• charn, ucharn, are respectively mapped on vec16i8 and vec16u8, where n=16. Other values of n are not supported.
• shortn, ushortn, are respectively mapped on vec16i16 and vec16i32, where n=16. Other values of n are not supported.
• intn, uintn, are respectively mapped on vec16i32 and vec16u32, where n=16. Other values of n are not supported.
• floatn, mapped on vec16f32, where n=16. Other values of n are not supported.

OpenCL Runtime Design

OpenCL APIs are a set of functions meant to coordinate and manage devices, those provide support for running applications and monitoring their execution. These APIs also provides a way to retrieve device-related information.

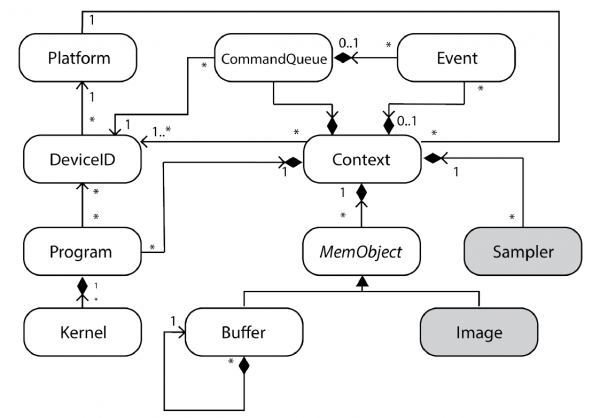
The following Figure depicts the UML Class diagram for the OpenCL Runtime as defined in the OpenCL specification. Grey-filled boxes represent not available features due to the absence of hardware support.

The custom OpenCL runtime relies on two main abstractions:

• Low-level abstractions, not entirely hardware dependent, provide device-host communication support.
• High-level abstractions, according to OpenCL APIs, administrate the life cycle of a kernel running onto the device.

OpenCL Example

The following code shows a vectorial matrix multiplication in OpenCL running on the nu+ device.

#include <opencl_stdlib.h>
#define WORK_DIM 4

__kernel void kernel_function(__global int16 *A, __global int16 *B, __global int16 *C, int rows, int cols)
{
   __private uint32_t threadId = get_local_id(0); 

   uint32_t nT = WORK_DIM; // number of threads
   uint32_t nL = 16;       // number of lanes

   uint32_t N = rows;
   uint32_t nC = N / nL;
   uint32_t ndivnT = N / nT;
   uint32_t tIdndivnT = threadId * ndivnT;
   uint32_t tIdndivnTnC = tIdndivnT * nC;
   for (uint32_t i = 0; i < ndivnT * nC; i++)
   {
       uint32_t col = (tIdndivnT + i) % nC;
       C[tIdndivnTnC + i] = 0;
       for (uint32_t j = 0; j < nC; j++)
       {
           for (uint32_t k = 0; k < nL; k++)
           {
               C[tIdndivnTnC + i] += A[tIdndivnTnC + i - col + j][k] * B[(nC * k) + (j * N) + col];
           }
       }
   }
}