Difference between revisions of "Programming Model"
(→NaplesPU Misc Intrinsics) |
|||
| Line 174: | Line 174: | ||
[[File:Intr.png]] | [[File:Intr.png]] | ||
| + | [[File:NPU_Intr.png]] | ||
== Learning by Example == | == Learning by Example == | ||
Revision as of 15:36, 19 June 2019
Contents
NaplesPU Programming Model
SIMD Support
Arithmetic operators (+, -, *, /, %), relational operators (==, !=, <, <=, >, >=), bitwise operators (&, |, ^, ~, <<, >>), logical operators (&&, ||, !) and assignment operators (=, +=, -=, *=, /=, %=, <<=, >>=, &=, ^=, |=) can be used with scalar and vector types and produce a scalar or vector signed integer result respectively. In some cases, mixed scalar/vector operations are possible. In such a cases, the scalar is considered as a vector with all elements equal to the scalar value.
For instance, to add two vectors:
#include <stdint.h>
int main (){
vec16i32 a;
vec16i32 b;
…
vec16i32 c = a+b;
}
or a vector with a scalar:
#include <stdint.h>
int main (){
vec16i32 a;
int b;
…
vec16i32 c = a+b;
}
In order to access vector elements, it is possible to use the operator []. For instance
#include <stdint.h>
int main (){
vec16i32 a;
// assign some values:
for (int i=0; i<16; i++) a[i]=i;
int sum = 0;
// calculate sum
for (int i=0; i<16; i++) sum += a[i];
}
Vectors can be initialized using curly bracket syntax. For instance, a constant vector:
#include <stdint.h>
int main (){
const vec16i32 a = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 };
}
or a non-constant vector
#include <stdint.h>
int main (){
int x, y, z;
...
vec16i32 a = { x, y, z, x, y, z, x, y, z, x, y, z, x, y, z, x};
}
Conversions between vectors with the same number of elements can be performed using the LLVM intrisic __builtin_convertvector. Vector types v16i32, v16u32, v16f32 can be converted between each other. Similarly, vector types v8i64, v8u64, v8f64can be converted between each other. For instance:
#include <stdint.h>
int main (){
vec16f32 a;
...
vec16i32 d = __builtin_convertvector(a,vec16i32);
}
It is also possible to convert floating point vectors with a different number of elements. In such a case, it is required to use the two NPU intrinsics __builtin_npu_v8f64tov16f32 or __builtin_npu_v16f32tov8f64. The first one converts 8 double precision FP elements into 8 single precision FP elements that are placed in the first 8 elements of a v16f32 vector. The second one converts the first 8 single precision FP elements of a v16f32 vector into 8 double precision FP elements. For instance:
#include <stdint.h>
int main (){
vec16f32 a;
...
vec8f64 b = __builtin_npu_v16f32tov8f64(a);
}
Vector comparisons can be done in two different ways. It is possible to use the traditional relational operators that result in another vector type of the same size of the two vectors. For instance:
#include <stdint.h>
int main (){
vec16i32 a;
vec16i32 b;
…
vec16i32 c = a < b;
}
After executing the above code, the vector c elements will be equal to 0xFFFFFFFF or 0x00000000 according to the result of the comparison. In addition, we also provide vector comparison intrinsics, as follow:
#include <stdint.h>
int main (){
vec16i32 a;
vec16i32 b;
…
int c = __builtin_npu_mask_cmpi32_slt (a, b)
}
After executing the above code, the integer c will contain a bitmap that can be directly used to write the mask register if required. Using vector comparison intrinsics is the natural way of performing comparisons in NaplesPU.
Note that, in NaplesPU, all instructions are masked and at the beginning, all lanes are enabled. If you want to handle SIMD control flow, you need to explicitly take care of masking operations so that they are only applied to some elements. For instance, take a look at the above code:
#include <stdint.h>
int main (){
vec16i32 a;
vec16i32 b;
…
int c = __builtin_npu_mask_cmpi32_slt (a, b) //generate mask for a<b
int rm_old = __builtin_npu_read_mask_reg(); //save mask register
__builtin_npu_write_mask_reg(c); //write mask register for a<b
do_something();
c = c^-1; //generate mask for a greater equal b
__builtin_npu_write_mask_reg(c); //write mask register for a greater equal b
do_somethingelse();
__builtin_npu_write_mask_reg(rm_old); //restore the old mask
}
Thread Parallelism
In a NPU core each thread runs the same code provided by the user, through builtins developers can parallelize it or differentiate flows. Each thread has a private stack, while the memory system is distributed and all threads have the same view of the main memory. User can differentiate threads flow based on the running thread ID, as described in control register each thread can read its ID from the control register through the __builtin_npu_read_control_reg accessing to the needed control register (for fetching thread ID use 2, for core ID use 0 or 1):
#define CORE_ID __builtin_npu_read_control_reg(0) #define THREAD_ID __builtin_npu_read_control_reg(2)
In the current release, each tile is equipped with 1 NPU core, hence each core ID overlaps with its tile ID.
Thread Synchronization
NaplesPU supports barrier synchronization among threads. The programmer needs to know the number of threads that require to synchronize, i.e. NumberOfThreads. For each synchronization, there is a unique barrier ID. The NaplesPU intrinsic __builtin_npu_barrier(BarrierID, NumberOfThreads-1) takes care of the synchronization. It is possible to exploit a maximum number of barriers equal to Bmax, i.e. 4 x number of threads. Barrier IDs range from 0 to Bmax-1. Note that, same barrier ID cannot be used in different kernels and can be used multiple times inside a kernel only by the same threads or by a subset of them.
In the following example, we have four threads and two barriers. After performing some operations, all threads synchronize on barrier 1. Then, only threads 0 and 1 synchronize on barrier 2. Remember that, in the main code, the user has to provide the total number of synchronizing threads:
#include <stdint.h>
static vec16i32 C[4];
static vec16i32 D[2];
const vec16i32 A[4]={{...} ,{...},{...}, {...}};
const vec16i32 B[4]={{...},{...},{...}, {...}};
int main(){
//execution thread 0,1,2,3
int threadId = __builtin_npu_read_control_reg(2);
C[threadId] = A[threadId] + B[threadId];
__builtin_npu_barrier(1,3);//Synchronization Threads:0,1,2,3.
if(threadId<2){
//execution thread 0,1
D[threadId]=C[threadId*2]+C[(threadId*2)+1];
__builtin_npu_barrier(2,1);//Synchronization Threads:0,1.
}
if(threadId==0){
D[threadId]=D[threadId]+D[threadId+1];
__builtin_npu_flush((int)(&D[threadId]));
}
return 0;
}
NaplesPU Other Aspects
Flush instruction
The NaplesPU ISA has a flush instruction that is required to avoid data to keep stuck in the cache. It is mandatory to use this instruction in case of output data that is required from the host. Otherwise, the host will read data from the main memory that is not coherent with the cache. The flush instruction takes in input the address of the involved variable and flushes an entire 512-bit cache line. Please remember to cast to integer the address, otherwise you will see the following error: “cannot initialize a parameter of type 'int' with an rvalue of type (YOUR VARIABLE TYPE)*'”. For instance, take a look at the above code:
#include <stdint.h>
int main (){
vec16i32 a;
vec16i32 b;
…
vec16i32 c = a + b;
__builtin_npu_flush((int)&c);
}
Please, remember that the flush instruction works for a single 512-bit cache line. As a consequence, multiple flush instructions are required in case of variable types bigger than 512 bits.
Scratchpad memory
In addition to traditional main memory, a NPU core supports a scratchpad memory with a different address space. In order to use the scratchpad memory, the __scratchpad keyword should be used when declaring a variable. Note that just a global variable can be placed in the scratchpad memory. For instance, take a look at the above code:
#include <stdint.h>
__scratchpad int a;
int main (){
...
}
The compiler will recognize the keyword and the integer a variable will be placed in the scratchpad using appropriate load/store instructions.
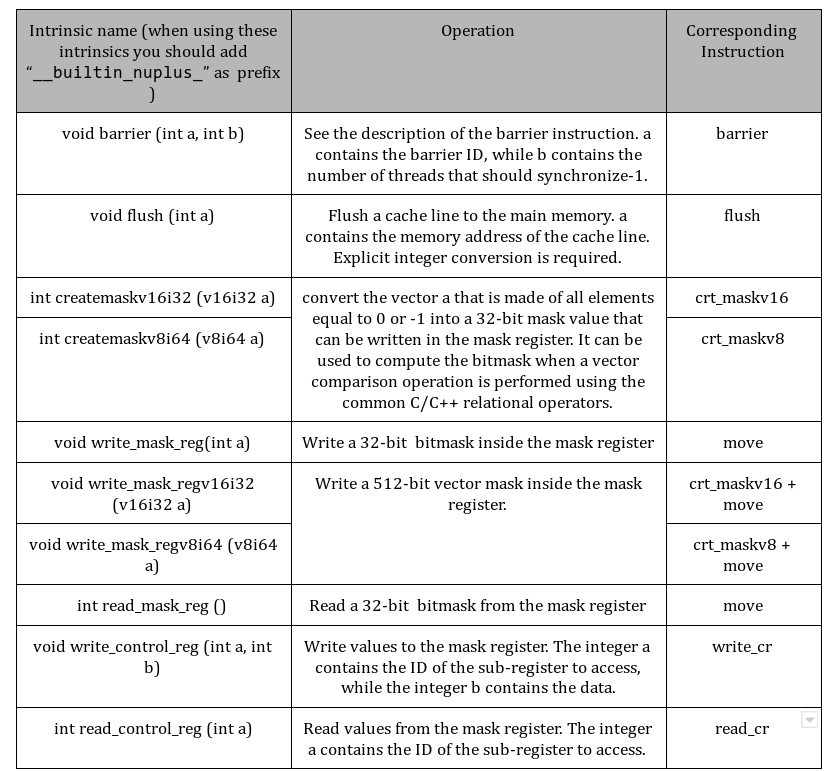
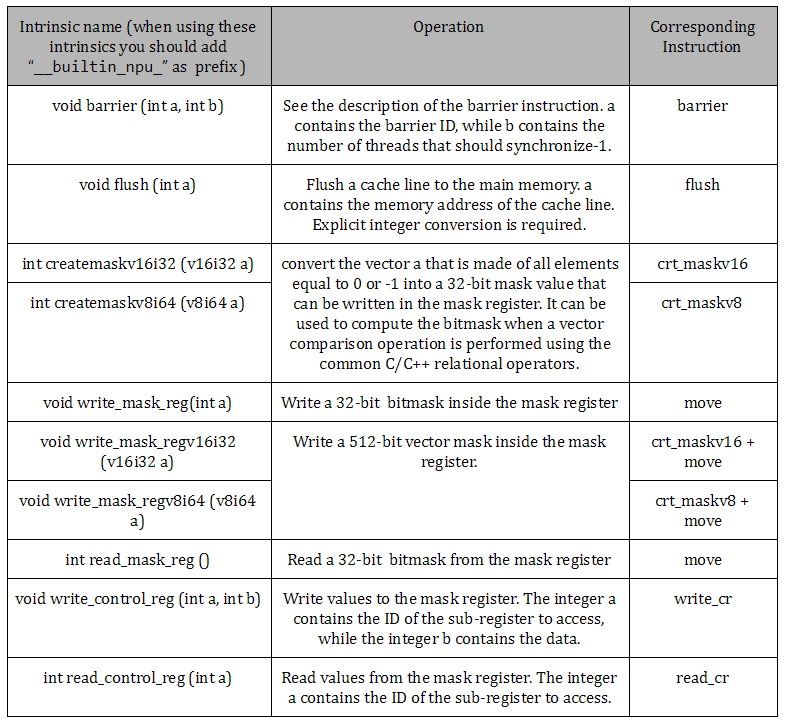
NaplesPU Misc Intrinsics
Main NaplesPU builtins are summarized in the following table:
Learning by Example
Matrix Multiplication Multithreaded Example
The following code shows a multithread version of the matrix multiplication kernel running on a NPU core. The code spreads the output computation among all available threads. Since each output element computation is independent of others, the thread parallelism is achieved dividing the outer cycle of the function. Output matrix row calculations are equally spanned across all cores and further spanned across threads. For each thread, the function first calculates the portion of the output matrix to compute at the core level: N / CORE_NUMB, with N the dimension of the matrix and CORE_NUMB the number of NPU core in the system.
Then, each thread starts computing the outer loop with start_loop = (core_id * N / CORE_NUMB) + thread_id the portion of output matrix to compute is multiplied to the running core ID (core_id) and added to the running thread ID (thread_id), and each iteration increments by the number of threads in the core THREAD_NUMB.
void matrix_mult(const int a[N][N], const int b[N][N], int mult[N][N], int core_id, int thread_id) {
int start_loop = (core_id * N / CORE_NUMB) + thread_id;
int end_loop = N / CORE_NUMB * (core_id + 1);
for (int i = start_loop; i < end_loop; i += THREAD_NUMB){
for (int j = 0; j < N; j++)
for (int k = 0; k < N; k++)
mult[i][j] += a[i][k] * b[k][j];
}
}
Parameters core_id and thread_id are passed by the main function, and fetched from NPU control registers through builtins:
#define CORE_ID __builtin_npu_read_control_reg(0) #define THREAD_ID __builtin_npu_read_control_reg(2)
In this way, each thread in each core computes a portion of the output matrix concurrently to the others.
The final result is ready when all thread over the system ended the assigned task, a system synchronization is required and in the main function this is achieved using barrier builtin provided by the programming model:
__builtin_npu_barrier(42, CORE_NUMB * THREAD_NUMB - 1);
The builtin above synchronizes CORE_NUMB * THREAD_NUMB number of threads (total number of thread running in the system) on the ID 42. When all threads hit the barrier the output matrix is ready, although most of it could be in private L1 caches. The next step is to flush output lines into the main memory:
if (THREAD_ID == 0 && CORE_ID == 0) {
for (int i = 0; i < N*N; i += 64 / sizeof(int)) {
__builtin_npu_flush((int) &C[i / N][i % N]);
}
__builtin_npu_write_control_reg(N*N, 12); // For cosimulation purpose
}
Generally, flush operations are performed by a thread, in this case the first thread in the first core calls the flush builtin which sends output results still in L1 caches to the main memory.
The full code for the main function is attached below:
#define CORE_ID __builtin_npu_read_control_reg(0)
#define THREAD_ID __builtin_npu_read_control_reg(2)
int main(){
init_matrix(A);
init_matrix(B);
matrix_mult(A, B, C, CORE_ID, THREAD_ID);
__builtin_npu_barrier(CORE_ID + 1, THREAD_NUMB - 1);
if (THREAD_ID == 0 && CORE_ID == 0) {
for (int i = 0; i < N*N; i += 64 / sizeof(int)) {
__builtin_npu_flush((int) &C[i / N][i % N]);
}
__builtin_npu_write_control_reg(N*N, 12); // For cosimulation purpose
}
return (int)&C;
}
Matrix Multiplication Vectorial Example
On the other hand, the vectorial version of the matrix multiplication function computes the output matrix in a SIMD multithreading fashion. Both input and output matrices are organized in target specific vector types, becoming vectors of vectors. Such an organization results in a distribution of the N column partial results on the 16 hardware lanes; each thread calculates N partial results every cycle. The size of the matrix must be multiple of 16.
void kernel_function(vec16i32 *A, vec16i32 *B, vec16i32 *C, int N) {
uint32_t coreId = __builtin_npu_read_control_reg(0);
uint32_t threadId = __builtin_npu_read_control_reg(2);
uint32_t nT = 2; // number of threads
uint32_t nL = 16; // number of lanes
uint32_t nC = N/nL;
uint32_t ndivnT = N/nT;
uint32_t tIdndivnT = threadId*ndivnT;
uint32_t tIdndivnTnC = tIdndivnT*nC;
for (uint32_t i = coreId; i < ndivnT*nC; i+=CORE_NUMB){
uint32_t col = (tIdndivnT+i)%nC;
C[tIdndivnTnC+i] = 0;
for (uint32_t j = 0; j < nC; j++){
for (uint32_t k = 0; k < nL; k++){
C[tIdndivnTnC+i] += A[tIdndivnTnC+i-col+j][k] * B[(nC*k)+(j*N)+col];
}
}
}
}
Please note, the C[tIdndivnTnC+i] += A[tIdndivnTnC+i-col+j][k] * B[(nC*k)+(j*N)+col] performs 16 operations on 16 different data at time. The organization of the code and the thread parallelization are equivalent to its scalar version.
How to compile a kernel
Currently, the NaplesPU toolchain is released with some example kernels located in the npu/software/kernels folder. We provide makefiles to compile these kernels for NaplesPU. In case you want to add a new kernel, it is suggested to copy a kernel folder and replace C/CPP files with your own source code. Then, remember to modify the makefile updating the SRCS variable with the current main C/CPP filenames.
OpenCL support for NaplesPU
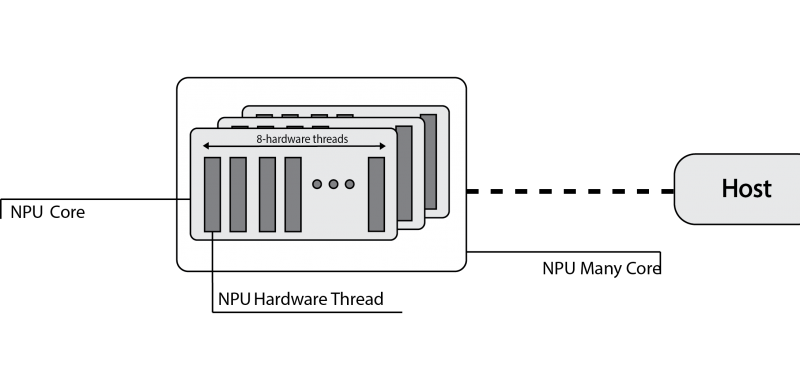
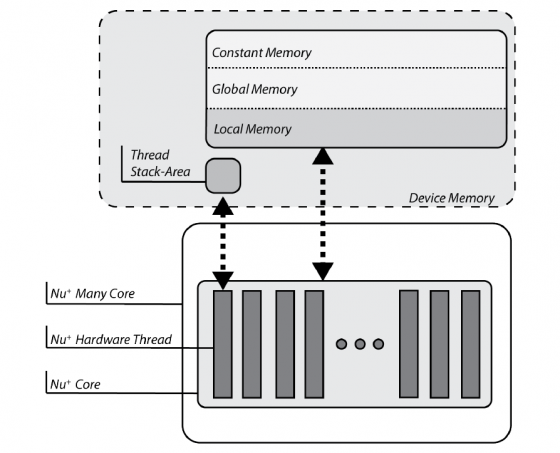
OpenCL defines a platform as a set of computing devices on which the host is connected to. Each device is further divided into several compute units (CUs), each of them defined as a collection of processing elements (PEs). Recall that the target platform is architecturally designed around a single core, structured in terms of a set of at most eight hardware threads. Each hardware threads competes with each other to have access to sixteen hardware lanes, to execute both scalar and vector operations on 32-bit wide integer or floating-point operands.
The computing device abstraction is physically mapped on the NaplesPU many-core architecture. The NaplesPU many-core can be configured in terms of the number of cores. Each NPU core maps on the OpenCL Compute Unit. Internally, the NPU core is composed of hardware threads, each of them represents the abstraction of the OpenCL processing element.
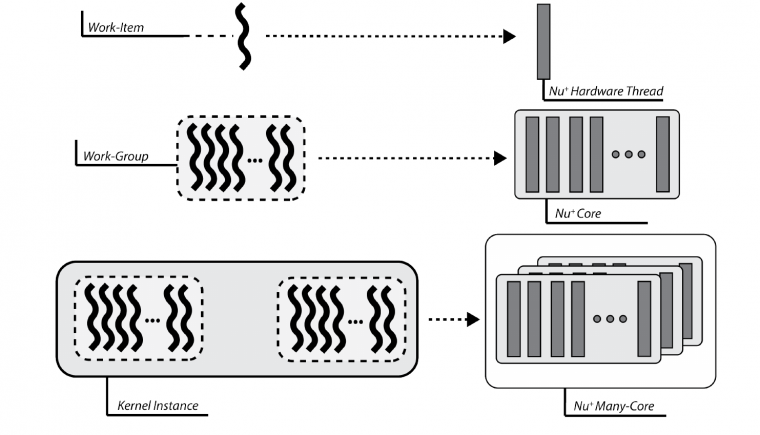
Execution Model Matching
From the execution model point of view, OpenCL relies on an N-dimensional index space, where each point represents a kernel instance execution. Since the physical kernel instance execution is done by the hardware threads, the OpenCL work-item is mapped onto a NPU single hardware-thread. Consequently, a work-group is defined as a set of hardware threads, and all work-items in a work-group executes on a single computing unit.
Memory Model Matching
OpenCL partitions the memory in four different spaces:
- the global and constant spaces: elements in those spaces are accessible by all work-items in all work-group.
- the local space: visible only to work-items within a work-group.
- the private space: visible to only a single work-item.
The target-platform is provided of a DDR memory, that is the device memory in OpenCL nomenclature. Consequently, variables are physically mapped on this memory. The compiler itself, by looking at the address-space qualifier, verifies the OpenCL constraints are satisfied.
Each NPU core is also equipped with a Scratchpad Memory, an on-chip non-coherent memory portion exclusive to each core. This memory is compliant with the OpenCL local memory features
Finally, each hardware thread within the NPU core has a private stack. This memory section is private to each hardware thread, that is the OpenCL work-item, and cannot be addressed by others. As a result, each stack acts as the OpenCL private memory.
Programming Model Matching
OpenCL supports two kinds of programming models, data- and task-parallel. A data-parallel model requires that each point of the OpenCL index space executes a kernel instance. Since each point represents a work-item and these are mapped on hardware threads, the data-parallel requirements are correctly satisfied. Please note that the implemented model is a relaxed version, without requiring a strictly one-to-one mapping on data.
A task-parallel programming model requires kernel instances are independently executed in any point of the index space. In this case, each work-item is not constrained to execute the same kernel instance of others. The compiler frontend defines a set of builtins that may be used for this purpose. Moreover, each NPU core is built of 16 hardware lanes, useful to realise a lock-step execution. Consequently, OpenCL support is realised to allow the usage of vector types. As a result, the vector execution is supported for the following data types:
- charn, ucharn, are respectively mapped on vec16i8 and vec16u8, where n=16. Other values of n are not supported.
- shortn, ushortn, are respectively mapped on vec16i16 and vec16i32, where n=16. Other values of n are not supported.
- intn, uintn, are respectively mapped on vec16i32 and vec16u32, where n=16. Other values of n are not supported.
- floatn, mapped on vec16f32, where n=16. Other values of n are not supported.
OpenCL Runtime Design
OpenCL APIs are a set of functions meant to coordinate and manage devices, those provide support for running applications and monitoring their execution. These APIs also provides a way to retrieve device-related information.
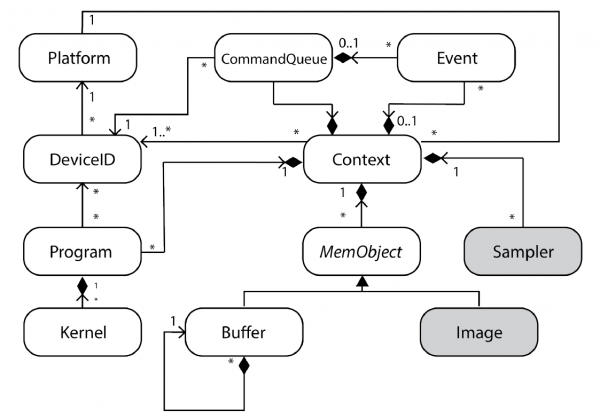
The following Figure depicts the UML Class diagram for the OpenCL Runtime as defined in the OpenCL specification. Grey-filled boxes represent not available features due to the absence of hardware support.
The custom OpenCL runtime relies on two main abstractions:
- Low-level abstractions, not entirely hardware dependent, provide device-host communication support.
- High-level abstractions, according to OpenCL APIs, administrate the life cycle of a kernel running onto the device.
OpenCL Example
The following code shows a vectorial matrix multiplication in OpenCL running on the NPU device.
#include <opencl_stdlib.h>
#define WORK_DIM 4
__kernel void kernel_function(__global int16 *A, __global int16 *B, __global int16 *C, int rows, int cols)
{
__private uint32_t threadId = get_local_id(0);
uint32_t nT = WORK_DIM; // number of threads
uint32_t nL = 16; // number of lanes
uint32_t N = rows;
uint32_t nC = N / nL;
uint32_t ndivnT = N / nT;
uint32_t tIdndivnT = threadId * ndivnT;
uint32_t tIdndivnTnC = tIdndivnT * nC;
for (uint32_t i = 0; i < ndivnT * nC; i++)
{
uint32_t col = (tIdndivnT + i) % nC;
C[tIdndivnTnC + i] = 0;
for (uint32_t j = 0; j < nC; j++)
{
for (uint32_t k = 0; k < nL; k++)
{
C[tIdndivnTnC + i] += A[tIdndivnTnC + i - col + j][k] * B[(nC * k) + (j * N) + col];
}
}
}
}